Autoregressive processes : learning with an interactive tool

I recently got interested in second order autoregressive processes ("AR(2)" processes), after spending quite some time working only with first order ones... It was time to get an extra degree of freedom/complexity ! However, I didn't have much intuition about the behavior of these models and neither about how to "tune the knobs" that set this behavior so I spent some time on this subject.

For the sake of clarity, let's write down a definition/notation for an AR(2) process X_k:

X_k = a_1 X_{k-1} + a_2 X_{k-2} + Z_k

with the real numbers a1 and a2 being the two parameters that tune the "behavior" of the process. Z_k may be call the "input" in the context of linear filters, while "innovation" (i.e. a white noise input) would better fit in the context of random processes. A nice property of AR(2) processes, as opposed to AR(1) is their ability to capture slowly oscillating behaviors, like ocean waves. Also, within the AR(2) model, AR(1) is included as the special case a2 = 0.

Bits of a non-interactive study

In order to understand the interplay of the two parameters a1 and a2, I spent extensive time doing paper-based analytical/theoretical studies. I also created a IPython Notebook which I should publish when there is proper Notebook -> HTML conversion system (edit: now available on nbviewer). Most of the AR(2) behavior is governed by the characteristic polynomial P(z) = z^2 - a_1 z - a_2. This polynomial helps in showing that there are two regimes : the one with two real roots (when a_2 > - a_1^2/4 ) and the one with two complex-conjugate roots (when a_2 < - a_1^2/4 ) where I can get my long-awaited slow oscillations. A third regime is the special case of a double root a_2 = - a_1^2/4 which I don't think is of a special interest.

Beyond the study of the root, I also computed the variance of the process and its spectral density. I found both not so easy to compute !

Creating an interactive tool

After the static paper-based study and the still semi-static computer-based study, where I was able to derive and plot the impulse response and some realization of random trajectories, I wanted to get a real-time interactive experience of the interplay of the two parameters a1 and a2. To this end I wrote a tiny Python script, based on the event handling machinery of Matplotlib. More specifically, I started from the "looking glass" example script which I altered progressively as my understanding of event handling in Matplotlib was getting better. Here is a frozen screen capture of the resulting plots:

screen capture from the Interactive AR2 demo
Interactive demo of some properties of an auto-regressive AR(2) process

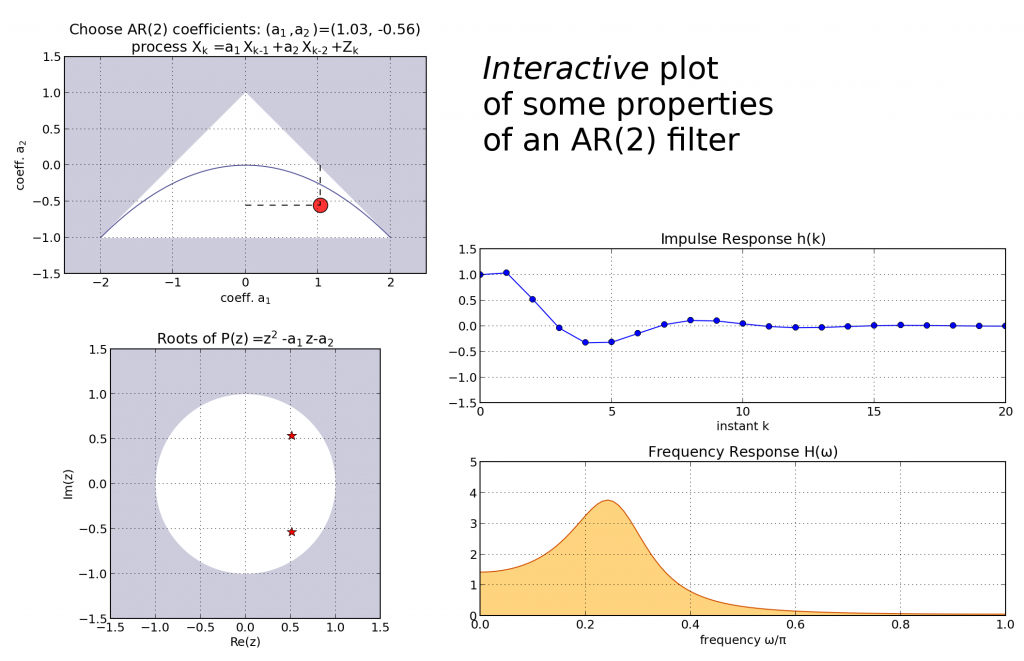
I put the code of this script on a GitHub Gist. This code is quite crude but it should work (assuming that you have NumPy, SciPy and Matplotlib installed). I've implemented the plots of three properties of the process:

  1. the root locus diagram, where one can see the transition between the two real roots and the two complex-conjugate roots as the a_2 = - a_1^2/4 boundary is crossed.
  2. the Impulse Response (output of the filter for a discrete impulse Z_k = \delta_k ), implemented simply using scipy.signal.lfilter.
  3. the Frequency Response, which I normalized using the variance of the process so that it always has unit integral. This latter property is mainly based on my own analytical derivations so that it should not be taken as a gold reference !

My feeling about interactive plotting with Matplotlib

Overall, I felt pretty at ease with the event handling machinery of Matplotlib. I feel that writing an interactive plot didn't add too many heavy lines of code compared to a regular static plot. Also, the learning curve was very smooth, since I didn't have to learn a new plotting syntax, as opposed to some of my older attempts at dynamic plotting with Traits and Chaco. Still, I feel that if I wanted to add several parameters in a small interactive GUI, Traits would be the way to go because I haven't seen a nice library of predefined widgets in Matplotlib (it's not it's purpose anyway). So I keep the Traits and Chaco packages for future iterations !

Author: pierre

assistant professor in Electrical Engineering & Control

3 thoughts on “Autoregressive processes : learning with an interactive tool”

  1. Your study is very interesting, and intuitive~

    Nowadays I'm also working with AR models,  actually trying to find the coefficients' behavior with respect to the signal's frequency content. Then I found out, the roots of  AR characteristic polynomial, are the the main components for the autocorrelation function of this AR process. And the frequency spectral density function is then the fourier transform of our autocorrelation function. So it seemed to me that the coefficients do have some influence on the frequency domain~

    As for the capture of oscillations, the real root of AR characteristic polynomial contribute to the autocorrelation function that has a exponential decaying shape (linear signal), and the complex root gave a exponentially damped oscillation. So I guess, while the order of AR model is 2 or above, there is the possibility that the characteristic polynomial will have a complex root, and therefore has the ability to describe a wave shaped signal, or say, a signal which has some more frequency content.

    But then, the behavior of 2nd order AR is hard enough to interpret，and I'm working with 4,5 or 8th order AR... kind of frustrated to find some one to one relation for AR coefficients and frequency components.

     

    Reply

    1. The AR coefficients have of course an influence on the spectral density : there are directly linked. I just found a quick reference on reference.wolfram.com which gives the formula for the spectrum of an ARMA.

      About the characteristic polynomial, you can indeed see on the plot that the two roots are complex conjugate when the behavior is oscillatory. That's why an order of at least two is required to get oscillations.

      The physical interpretation of coefficients for a discrete time model is alway difficult, but much better with continuous time models. Also, for higher order models, it is always possible to factorize the polynomials as a product of first or second order terms.

      Reply

Leave a Reply

Your email address will not be published. Required fields are marked *