Tag: convex optimization

Convex Storage Loss Modeling for Optimal Energy Management

I’ve put online (on HAL) the manuscript I’ve submitted to PowerTech 2021 (⚠ not yet accepted [Edit: it was eventually accepted. Presentation video is available]). It discusses the modeling of energy storage losses. The question is how to model these losses using convex functions, so that the model can be embedded efficiently in optimal energy management problems.

Key idea

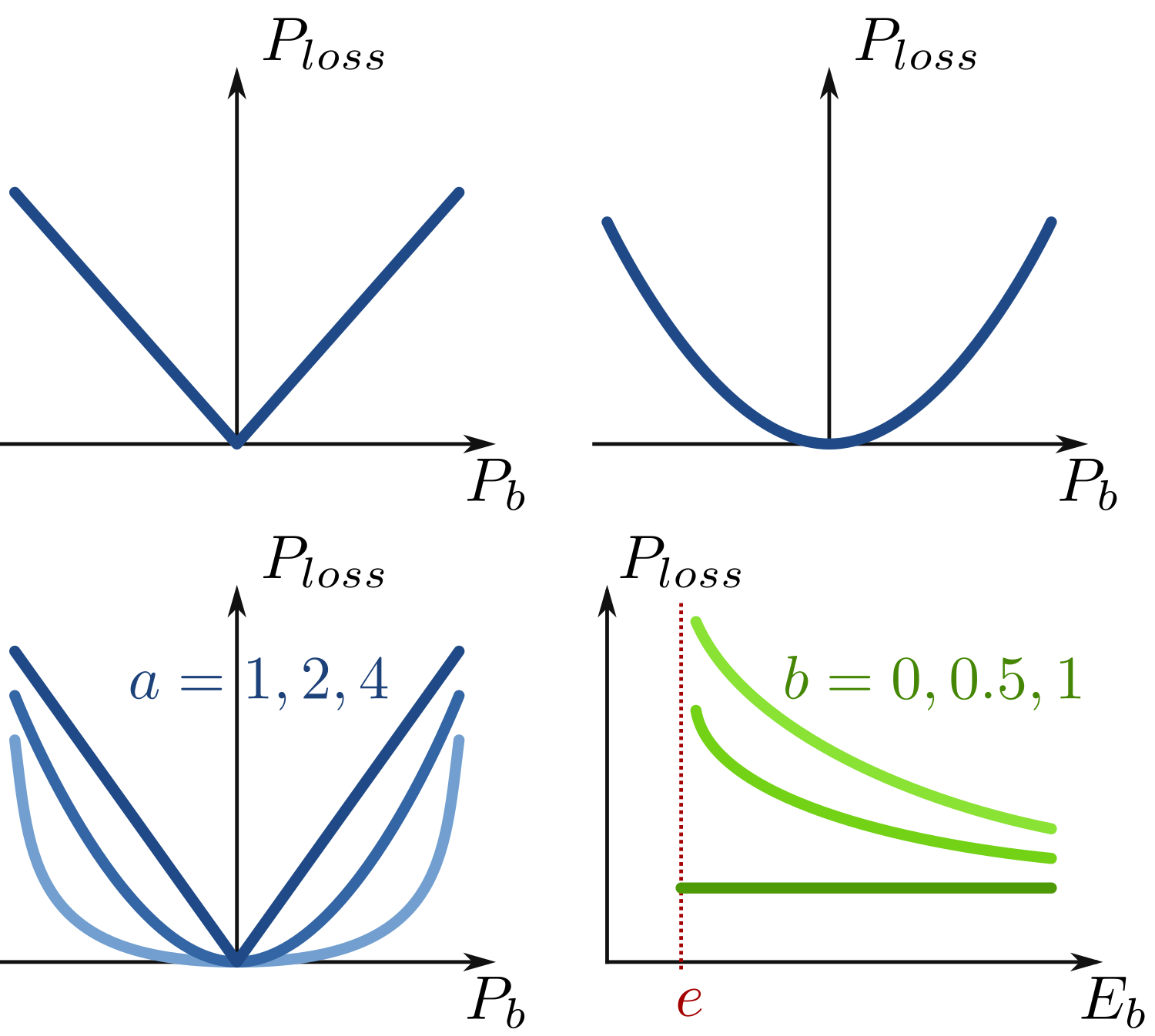
This is possible thanks to a constraint relaxation: losses are assumed to be greater than (≥) their expression, rather than equal (=). With a convex loss expression, the resulting constraint is convex. In applications where energy losses tend to be naturally minimized, this works great. This means that the inequality is tight at the optimum: losses are eventually equal to their expression. Notice that in applications where dissipating energy can be necessary at the optimum, this relaxation can fail: losses are strictly greater than their expression, meaning that there are extraneous losses!

Germination

I’ve had this topic in mind for some years now, with early discussion at PowerTech 2015 with Olivier Megel (then at ETH Zurich). Fast-forwarding to spring 2020, I had a nice exchange with Jonathan Dumas and Bertrand Cornélusse (Univ. Liège) which provided me with related references in the field of power systems.

After some experiments at the end of the last academic year, I’ve assembled these ideas during the autumn (conference deadline effect), realizing that, as often, there was quite a large amount of literature on the topic. Papers that I would have stayed unaware of, if not writing the introduction of this paper! Still, I found the subject was not exhausted (also a common pattern) so that I could position my ideas.

Contribution

I believe that the contribution is:

  1. Describe the relaxation of storage losses in a unified way which handles the various existing loss models
  2. Provide a simple continuous family of nonlinear convex loss expressions which can depend on both storage power and energy level.

The typical effect being covered by the loss model I propose is when power losses (proportional to the squared power) varies with the state of charge (typically at the very end of charge or discharge). In short, it unites and generalizes classical loss models, while preserving convexity.

I don’t think this will revolutionize the field, but hopefully it can help people in energy management using physically more realistic battery models, while still keeping the computational efficiency of convex optimization.

Plot of storage loss functions of storage power or storage energy
Classical loss models (above) are piecewise linear (e.g. constant efficiency) or quadratic in storage power (Pb). Few models also depends on the storage energy level (Eb). The proposed model unites and generalizes classical loss models, while preserving convexity. See manuscript for the meaning of parameters a and b.