Tag: energy storage

Battery State of Charge estimation with Kalman filter - Python implementation

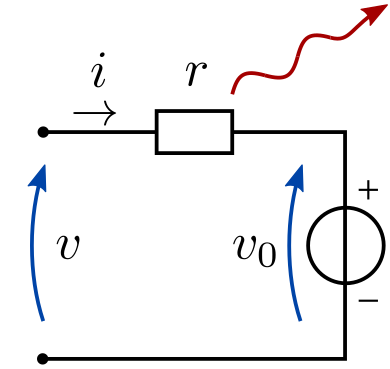
At the VéloMix hackathon at IMT Atlantique in Rennes, I met with Guillaume Le Gall (ESIR, Univ Rennes) and Matthieu Silard (IMT Atlantique) working on battery charging monitoring. We ended up working on the problem of State of Charge (SoC) estimation, that is evaluating the charge level of a battery by monitoring its voltage and current along time (and notably not its open circuit voltage).

simple battery equivalent circuit model with open circuit voltage (OCV) + resistive voltage drop

I had heard SoC estimation was often performed by the Kalman filter (and in particular with EKF, its extended version), but I had never had the occasion to implement it. Time was too short to get it working on the day of the hackathon, but now I have drafted a Python implementation, or more precisely three implementations:

  1. Step-by-step literate programming version of the filter, using a sequence of notebook cells, to implement one step of the filter → Nice to see the algorithm crunching the data line-by-line
  2. Generic Kalman filter implementation (all the above steps wrapped in a single function, should work with any state space model)
  3. Compact implementation specialized for SoC estimation with baked-in battery model (this last one should be the most useful to project, ready to convert to Arduino/C++ code)

All these are available in a single Jupyter notebook:

Présentation « Optimisation des microréseaux » @ENS Rennes

(Post in French, since it’s about a presentation in French...)

Ma présentation « Optimisation des microréseaux » faite à l’École normale supérieure de Rennes pour les Rencontres Mécatroniques est disponible en ligne. À destination des étudiant.e.s en mécatronique, elle se voulait assez pédagogique pour expliquer les enjeux de dimensionnement et gestion d’énergie des systèmes énergétiques.

Présentation « Optimisation des microréseaux » @ENS Rennes (27’ présentation + questions).
Pas facile de se ré-entendre avec tout ses tics de parole !

Beaucoup d’idée développées dans le cadre de la thèse d’Elsy El Sayegh (soutenue mars 2024) avec mon collègue Nabil Sadou et qu'on continue à explorer avec Jean NIKIEMA, nouveau doctorant de l’équipe AUT !

Convex Storage Loss Modeling for Optimal Energy Management

I’ve put online (on HAL) the manuscript I’ve submitted to PowerTech 2021 (⚠ not yet accepted [Edit: it was eventually accepted. Presentation video is available]). It discusses the modeling of energy storage losses. The question is how to model these losses using convex functions, so that the model can be embedded efficiently in optimal energy management problems.

Key idea

This is possible thanks to a constraint relaxation: losses are assumed to be greater than (≥) their expression, rather than equal (=). With a convex loss expression, the resulting constraint is convex. In applications where energy losses tend to be naturally minimized, this works great. This means that the inequality is tight at the optimum: losses are eventually equal to their expression. Notice that in applications where dissipating energy can be necessary at the optimum, this relaxation can fail: losses are strictly greater than their expression, meaning that there are extraneous losses!

Germination

I’ve had this topic in mind for some years now, with early discussion at PowerTech 2015 with Olivier Megel (then at ETH Zurich). Fast-forwarding to spring 2020, I had a nice exchange with Jonathan Dumas and Bertrand Cornélusse (Univ. Liège) which provided me with related references in the field of power systems.

After some experiments at the end of the last academic year, I’ve assembled these ideas during the autumn (conference deadline effect), realizing that, as often, there was quite a large amount of literature on the topic. Papers that I would have stayed unaware of, if not writing the introduction of this paper! Still, I found the subject was not exhausted (also a common pattern) so that I could position my ideas.

Contribution

I believe that the contribution is:

  1. Describe the relaxation of storage losses in a unified way which handles the various existing loss models
  2. Provide a simple continuous family of nonlinear convex loss expressions which can depend on both storage power and energy level.

The typical effect being covered by the loss model I propose is when power losses (proportional to the squared power) varies with the state of charge (typically at the very end of charge or discharge). In short, it unites and generalizes classical loss models, while preserving convexity.

I don’t think this will revolutionize the field, but hopefully it can help people in energy management using physically more realistic battery models, while still keeping the computational efficiency of convex optimization.

Plot of storage loss functions of storage power or storage energy
Classical loss models (above) are piecewise linear (e.g. constant efficiency) or quadratic in storage power (Pb). Few models also depends on the storage energy level (Eb). The proposed model unites and generalizes classical loss models, while preserving convexity. See manuscript for the meaning of parameters a and b.

PowerTech 2015 article online

The article I submitted to PowerTech 2015 (Eindhoven, June 2015) has been accepted. I've put online the pdf manuscript. It is an author version, since the copyright will be transfered to IEEE.

Title: "Energy Storage Control with Aging Limitation"

[Update July 7, 2015] presentation slides are now also available.

Abstract

Energy Storage Systems (ESS) are often proposed to mitigate the fluctuations of renewable power sources like wind turbines. In such a context, the main objective for the ESS control (its energy management) is to maximize the performance of the mitigation scheme.

However, most ESS, and electrochemical batteries in particular, can only perform a limited number of charge/discharge cycles over their lifetime. This limitation is rarely taken into account in the optimization of the energy management, because of the lack of an appropriate formalization of cycling aging.

We present a method to explicitly embed a limitation of cycling aging, as a constraint, in the control optimization. We model cycling aging with the usual ``exchanged energy'' counting method. We demonstrate the effectiveness of our aging-constrained energy management using a publicly available wind power time series. Day-ahead forecast error is minimized while keeping storage cycling just under an acceptable target level.

Big Batteries Needed ?

From Big Batteries Needed To Make Fickle Wind And Solar Power Work, on NPR :

You can think of a fully charged battery as a source of energy, ready to sell its product to the electric grid, just the way a power plant does. For that to work, battery owners would need to buy electricity to charge the battery when the price is low, and then sell that electricity back to the grid when the price is high.

But that idea turns out to be a dud.

Not many articles in mass media or in scientific journals take the time to explain how useful batteries can be to integrate renewables. But fewer also explains, like this NPR post, that batteries, at their current cost and capabilities, are not ready for the massive deployment on the grid that is predicted by some.

Fortunately, there is much on-going research on battery technology (and on other storage technologies as well). The progress on batteries has been tremendous and steady since their invention (e.g. the impressive improvement of electric model aircraft since 70s), so there may still be technological leaps to come.