Now that I'm back from SGE 2018 conference, I've put online the manuscript of my article and the slides of my presentation (in French).
“Gestion d'énergie avec entrées incertaines :
quel algorithme choisir ?
Benchmark open source sur une maison solaire”
The title in English (translation of the whole article in progress...) is:
“Energy management with uncertain inputs:
which algorithms ?
Open source benchmark based on a solar home”
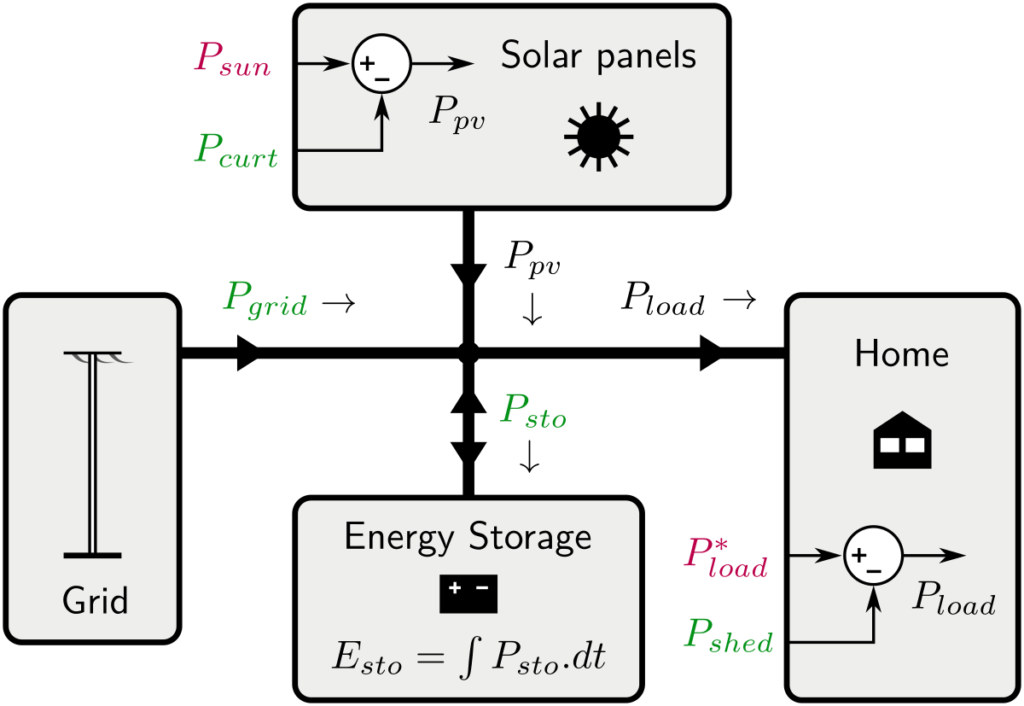
Here is the model of the solar home (power flows)
I've also a first translation of the abstract:
“Optimal management of energy systems requires strategies based on optimization algorithms. The range of tools is wide, and each tool calls on various theories (convex, dynamic, stochastic optimization...) which each require a period of appropriation ranging from a few days to several months.
It is therefore difficult for the novice energy management practitioner to
understand the main characteristics of each approach so we can compare them objectively and finally find the method or methods best suited to a given problem.
To facilitate an objective and transparent comparison, we propose an exemplary and simple energy management problem: a solar house with photovoltaic production and storage. After justifying the sizing of the system, we illustrate the benchmark by a first comparison of some energy management methods (heuristic rule, MPC and anticipatory optimization). In particular, we highlight the effect of the uncertainty of solar production on performance.
This benchmark, including the management methods described,
is open source, accessible online and multi-language (Python, Julia and Matlab).”
Access to the benchmark
The entire source code and the data (an extract from the Solar home electricity dataset by Ausgrid) is available on GitHub:
https://github.com/pierre-haessig/solarhome-control-bench/
As of now, only rather simple energy management methods are implemented, but I'd like to add some kind of stochastic MPC (once I've clarified what this really means), and later Stochastic Dynamic Programming.

